Gradient updates in logistic regression for binary classification Link to heading
- Predicted probabilities, $\hat{y}$, and Sigmoid function $\sigma (\cdot)$
For an example $i$, we have feature vector $\vec{x_{i}} = [x_{i1} , x_{i2} , \dots , x_{ip} ]^{T}$:
$$ z_i = \vec{w}^T \cdot \vec{x}_i + b $$
$$ \hat{y}_i = \sigma(z_i) = \frac{1}{1+e^{-z_i}} = \frac{1}{1+e^{-\vec{w}^T \vec{x}_i-b}} \in [0,1] $$
General estimated probabilities or likelihood of observing the data $(\vec{x}_i, y_i)$:
$$ \Pr(y_i | \vec{x}_i) = \hat{y_i}^{y_i} \cdot (1-\hat{y}_i)^{1-y_i} $$
$$ \Pr(y_i | \vec{w}, \vec{x}_i) = (\frac{1}{1+e^{-\vec{w}^T\vec{x}_i - b}})^{y_i} \cdot (\frac{e^{-\vec{w}^T\vec{x}_i-b}}{1 + e^{\vec{w}^T \vec{x} - b }})^{1-y_i} $$
- Entire dataset with $N$ samples, that likelihood (MLE) and its log likelihood (for convience):
$$ L = \prod_{i=1}^N \Pr(y_i | x_i) = \prod_{i=1}^N (\frac{1}{1+e^{-\vec{w}^T\vec{x}_i - b}})^{y_i} (\frac{e^{-\vec{w}^T\vec{x}_i+b}}{1 + e^{-\vec{w}^T \vec{x} -b }})^{1-y_i} $$
$$ \log L = \sum_{i=1}^N [ y_i \log(\hat{y}_i) + (1-y_i)\log(1-\hat{y}_i) ] $$
- Max log-likelihood = Min negative log-likelihood
$$ Loss(y, \hat{y}) = - \log L = - \sum_{i=1}^N [ y_i \log(\hat{y}_i) + (1-y_i)\log(1-\hat{y}_i) ] $$
Why? MLE aims to maximize $L$ by finding the $W$ and $b$ params that make the $\Pr(y|x)$ most likely. But gradient descent is for minimization problem for loss function, so we want a negative log likelihood.
- Training loss for an example and gradients
$$ \vec{w}^{*} = \arg\min_{\vec{w}} Loss(\vec{w}) $$
If we have $p$ features, we have $p$ parameters for the $\vec{w}$ which is $[w_1, w_2, \cdots, w_p]$. To minimize our cost function, we need to run the gradient descent on each parameter. We need to update each parameter simultaneously for each training sample $(O(N \times p)$) if brute force.
For $\vec{x}_i$ in $X$ ($N$ samples), and then for $\vec{w}_j$ in $W$ ($p$ features) with the first set of parameters initialized.
- Calculate $\hat{y}_i$
- Gradient for each $w_j$
$$ \frac{\partial Loss(\vec{w})}{\partial w_j} = \frac{\partial Loss}{\partial \hat{y_i}} \frac{\partial \hat{y_i}}{\partial z_i} \frac{\partial z_i}{\partial w_j} = - \sum_{i=1}^{N} [\frac{y_i}{\hat{y_i}} - \frac{1-y_i}{1-\hat{y_i}}] \cdot \hat{y_{i}} (1-\hat{y_{i}} ) \cdot x_{i,j} = - \sum_{i=1}^{N} (y_{i} - \hat{y_{i}} ) x_{i, j} $$
- Update
$$ w_{j} = w_{j} - \eta \frac{\partial Loss(\vec{w})}{\partial w_{j}} = w_{j} - \eta \sum_{i=1}^{N} (y_{i} - \hat{y_{i}} ) x_{i, j} $$
Binary-class with gradient descent on log loss Link to heading
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, roc_curve, roc_auc_score, log_loss, confusion_matrix
import matplotlib.pyplot as plt
from ucimlrepo import fetch_ucirepo, list_available_datasets
import numpy as np
np.random.seed(123)
data = fetch_ucirepo(id=17)["data"]
X = data.features
y = np.array(data.targets["Diagnosis"].apply(lambda x: 1.0 if x=="M" else 0.0))
X_train, X_valid, y_train, y_valid = train_test_split(X, y, test_size=0.25, stratify=y)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_valid = scaler.transform(X_valid)
def cross_binary_log_loss(y_real, y_pred):
epsilon = 1e-15
y_pred = np.clip(y_pred, epsilon, 1.0 - epsilon) # to avoid log(0)
return - (y_real * np.log(y_pred) + (1.0 - y_real) * np.log(1.0 - y_pred))
def gradient_loss_wrt_wj_bj(y_real, y_pred, x_ij):
grad_wj = np.sum((y_pred - y_real) @ x_ij)
grad_bj = np.sum((y_pred - y_real))
return grad_wj, grad_bj
def sigmoid(z):
if z >= 10:
z = 10
elif z <= -10:
z = -10
return 1 / (1 + np.exp(-z))
# for plotting:
list_total_logloss = []
# initialize weight params
weight_vector = np.random.random(X_train.shape[1])
bias_scalar = np.random.random(1)
lr = 0.001
epochs = 100
# multiple iterations/epochs
for epoch in range(epochs):
print()
print("epoch", epoch)
avg_logloss_epoch = 0
# one iteration:
for j, w in enumerate(weight_vector):
total_logloss = 0
y_pred = np.empty(0)
x_ij_vector = np.empty(0)
for i, x_i in enumerate(X_train):
z_i = weight_vector @ x_i + bias_scalar
y_pred_i = sigmoid(z_i)
# y_pred_i = 1.0 if y_pred_i_proba >= 0.5 else 0.0
# for each sample:
logloss = cross_binary_log_loss(y_train[i], y_pred_i)
total_logloss += logloss
# for gradient update later
y_pred = np.append(y_pred, y_pred_i)
x_ij_vector = np.append(x_ij_vector, x_i[j])
# update
grad_wj, grad_bj = gradient_loss_wrt_wj_bj(y_train, y_pred, x_ij_vector)
weight_vector[j] = w - lr*grad_wj
bias_scalar = bias_scalar - lr*grad_bj
print(f"feature {j}", total_logloss)
avg_logloss_epoch += total_logloss / len(weight_vector)
list_total_logloss.append(avg_logloss_epoch)
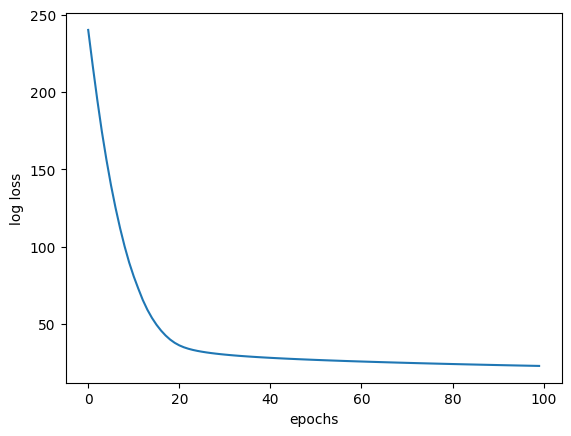
plt.plot(range(epochs), list_total_logloss)
plt.xlabel("epochs")
plt.ylabel("log loss")
epoch 0
feature 0 [253.85308605]
feature 1 [252.69318705]
feature 2 [252.03818375]
feature 3 [251.07456108]
feature 4 [250.15459244]
feature 5 [248.98802294]
feature 6 [248.14251822]
feature 7 [247.92729866]
feature 8 [247.73413734]
feature 9 [246.93601619]
feature 10 [243.60945911]
feature 11 [243.42557551]
feature 12 [242.90870849]
.
.
.
feature 13 [22.80782659]
feature 14 [22.80639194]
feature 15 [22.80471531]
feature 16 [22.80238045]
feature 17 [22.80106792]
feature 18 [22.80102124]
feature 19 [22.79703826]
feature 20 [22.7935156]
feature 21 [22.7926811]
feature 22 [22.78887515]
feature 23 [22.78829565]
feature 24 [22.78740452]
feature 25 [22.7794603]
feature 26 [22.77945808]
feature 27 [22.77101519]
feature 28 [22.76919309]
feature 29 [22.76589384]
Text(0, 0.5, 'log loss')
# validation
pred_total_logloss = 0
y_pred = np.empty(0)
z_pred = X_valid @ weight_vector + bias_scalar
for idx, z_i in enumerate(z_pred):
y_pred_i_proba = sigmoid(z_i)
y_pred_i = 1.0 if y_pred_i_proba > 0.5 else 0.0
y_pred = np.append(y_pred, y_pred_i)
logloss = cross_binary_log_loss(y_valid[idx], y_pred_i)
pred_total_logloss += logloss
print(pred_total_logloss)
print("portion of incorrect classification:", np.sum(y_pred != y_valid) / y_valid.shape[0])
207.23585675918488
portion of incorrect classification: 0.04195804195804196
Multi-class Link to heading
For multi-classification, logistic regression would use softmax function to convert the raw values into probabilities.
Forward pass and softmax ($C$ is the number of classes, and $z_c$ is the logit for class $c$): compute the logits ($z$) from the input features $$\Pr(y_i = c \mid x) = \frac{e^{z_c}}{\sum_{j=1}^C e^{z_j}}$$
Prediction: for a given example, choose the class with the highest probability: $$\hat{y} = \arg\max(\Pr)$$
Loss – categorical cross-entropy log loss for training ($y_c$ is the one-hot encoded label (1 if the sample belongs to class $c$, else 0): $$Loss = - \sum_{c=1}^C y_c \log(\hat{y}_c)$$
Gradient update: $$\frac{\partial Loss}{\partial w_j} = \frac{\partial \text{Loss}}{\partial z_c} \frac{\partial z_c}{\partial w_j} = \sum_{c=1}^C \sum_{i=1}^N (\hat{y}{c, i} - y{c, i})\cdot x_{i, j} $$ $$w_j = w_j - \eta \cdot \frac{\partial Loss}{\partial w_j}$$
Since it would take quite some time to implement these from scratch, I followed the sklearn code.
from sklearn.linear_model import LogisticRegression, LogisticRegressionCV
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, roc_curve, roc_auc_score, log_loss, confusion_matrix
from ucimlrepo import fetch_ucirepo, list_available_datasets
heart_disease = fetch_ucirepo(id=45)
X = heart_disease.data.features
y = heart_disease.data.targets
mice_imputer = IterativeImputer(random_state=123) # must have no NaNs
X = mice_imputer.fit_transform(X)
X_train, X_valid, y_train, y_valid = train_test_split(
X, y, stratify=y,
test_size=0.25, random_state=123)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_valid = scaler.transform(X_valid)
multi_class_model = LogisticRegression(
penalty = "l2", # l2 supports multinominal
tol = 0.0001,
C = 0.01, # smaller values imply stronger regularization, reduce overfitting
class_weight = "balanced",
random_state = 123,
solver = "lbfgs",
max_iter = 200,
# multi_class = "multinomial", # API changed
verbose = 0
)
# multi_class_model = LogisticRegressionCV(
# cv=5,
# penalty = "l2",
# tol = 1e-4,
# # C = 1.0,
# class_weight = None,
# random_state = 123,
# solver = "lbfgs",
# max_iter = 200,
# # multi_class = "multinomial", # API changed
# verbose = 0
# )
multi_class_model.fit(X_train, y_train)
y_preds = multi_class_model.predict(X_valid)
y_preds_probs = multi_class_model.predict_proba(X_valid)
accuracy = accuracy_score(y_valid, y_preds)
precision = precision_score(y_valid, y_preds, average='weighted')
recall = recall_score(y_valid, y_preds, average='weighted')
f1 = f1_score(y_valid, y_preds, average='weighted')
roc_auc = roc_auc_score(y_valid, y_preds_probs, multi_class='ovr')
print(accuracy, precision, recall, f1, roc_auc)
multi_class_model.coef_ # (n_classes, n_features)
0.5921052631578947 0.561654135338346 0.5921052631578947 0.5594253219080089 0.7682059222370341
array([[-0.08843996, -0.10681667, -0.21039802, -0.02031334, -0.0129146 ,
-0.01217517, -0.07925308, 0.13936476, -0.13266781, -0.14694061,
-0.08734563, -0.21866621, -0.18266378],
[-0.00627953, 0.03609585, -0.0142747 , 0.00220479, 0.00758366,
-0.04470998, -0.01094598, 0.01914847, 0.00836041, -0.10161291,
-0.08410252, -0.0787852 , -0.03746149],
[ 0.02179476, 0.03913942, 0.09711474, -0.04146647, 0.06054844,
0.12798226, -0.05106097, -0.06621271, 0.05177281, 0.06740908,
0.00811835, 0.04009986, 0.0677462 ],
[-0.09880347, -0.0062584 , 0.05792577, 0.00400038, -0.05066756,
0.06595486, 0.00230296, -0.09269345, 0.06455014, 0.03969532,
0.0484704 , 0.06538833, 0.10801748],
[ 0.17172819, 0.0378398 , 0.06963221, 0.05557464, -0.00454994,
-0.13705198, 0.13895706, 0.00039293, 0.00798446, 0.14144912,
0.1148594 , 0.19196322, 0.04436159]])
Given a new instance with a feature vector:
- Repeat the same dot product for all classes to get logits for each class (coef_i @ feature_vector for each logit $i$)
- the softmax function gives the probabilities for each class, and the model selects the class with the highest probability as the prediction.